A primeira parte do projeto consiste em projetar exatamente o que deveria ser feito. Como diz a sabedoria popular, “medir duas vezes, cortar uma só!”
Para elaboração do projeto eu fiz uso do aplicativo Google SketchUp 8.0 pois é o que consegui mais facilmente emular com Wine no Linux.
“Ah, por que você não usa Windows?!”
- Porque não presta!
“Ah, por que você não tentou emular uma versão mais recente?!”
- Lei do menor esforço. Esta já estava pronta para instalar e usar.
Cálculo da área total do tablado e seu desenho
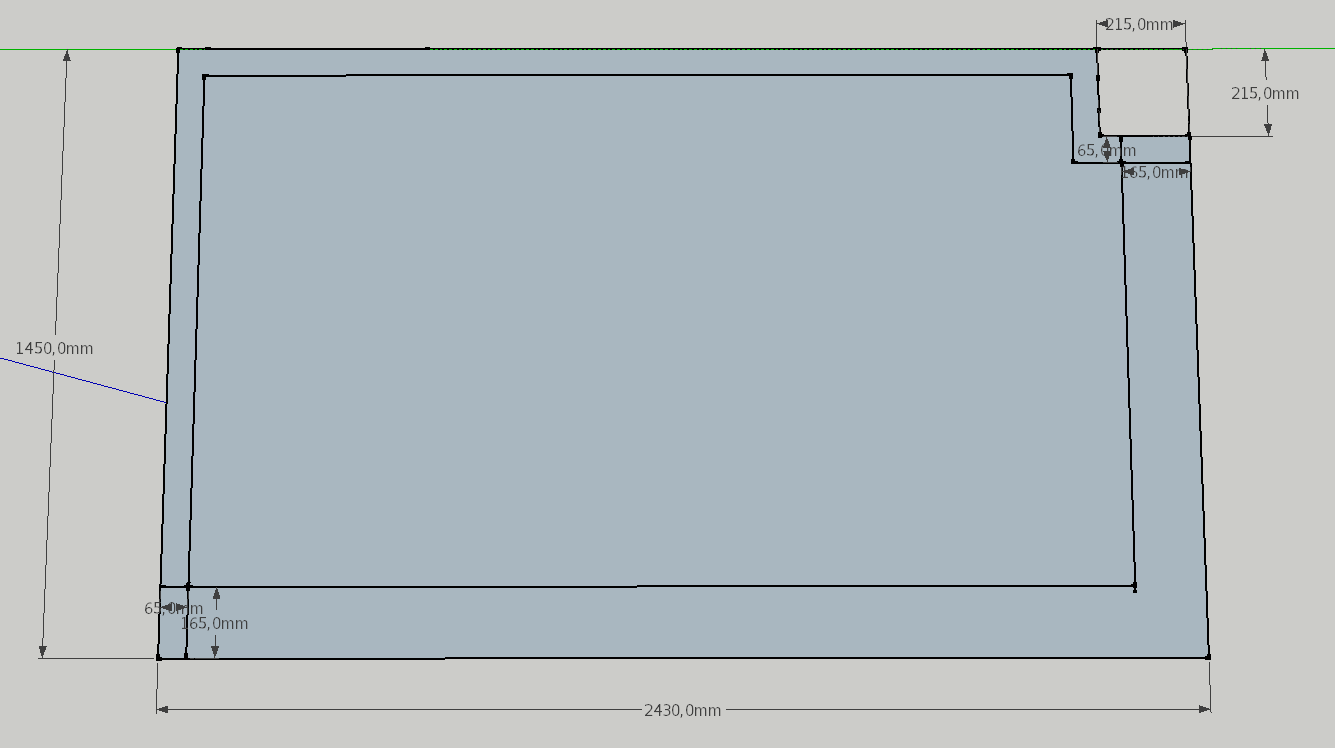
Certo, as primeiras medidas que tirei foram as do espaço onde iria instalar o tablado (neste caso a sacada do meu apartamento), que mede 2430mm por 1450mm (converte pra metro, te vira!). Além disso, devido a um espaço para a descida do cano do ralo de todas as sacadas do prédio, em um dos cantos uma área de 215mm por 215mm deveria ser desconsiderada. Sendo assim, a área para a instalação do tablado seria conforme abaixo:
Figura 2 - Área destinada à instalação do tablado
Nas faces do lado direito e inferior da Figura 2, a sacada possui um fechamento com vidro que por vezes apresenta infiltrações permitindo a entrada de água. Para isso foi destinado um espaço de 165mm nestas faces e nas demais um espaço de 65mm apenas para que o tablado não encostasse na parede transferindo, assim, as vibrações cujo intuito era o de absorver.
A indagação que pulula em sua mente neste momento é: “Entendi tudo até agora, mas por que exatamente 65mm e 165mm?!”
O que? Não é esta a indagação? Deveria! Aprenda a fazer perguntas mais pertinentes…
O espaço inicial que seria destinado era o de 50mm nos lados com parede convencional e 15mm nos lados fechados com vidro. Entretanto, as chapas de compensado possuem comprimento de 2200mm. Logo:
2430mm - 50mm - 150mm = 2230 (sobraram 30mm, já que o comprimento é de 2200mm)
30mm/2 = 15mm para cada lado.
Portanto: 50mm + 15mm = 65mm; e
150mm + 15mm = 165mm.
Entendeu?
O mesmo cálculo foi feito para a largura, entretanto, tendo a largura original das chapas a medida de 1600mm e tendo a sacada a largura total de 1450mm, logicamente as chapas seriam maiores nesta dimensão que o espaço disponível. Sendo assim, era necessário calcular onde deveriam ser cortadas as chapas para o tamanho adequado. Então:
1450mm - 50mm - 150mm = 1250mm.
Sendo assim, as chapas de compensado deveriam possuir dimensões finais de 2200mm x 1250mm.
Mas nem tudo são flores nesta vida, é ou não é?! Você, leitor atento, recorda-se da área perdida para o espaço por onde corre o cano d’água com o dreno de todas as sacadas do prédio? Pois é, perspicaz legente! Precisaríamos fazer a conta do quanto seria removido das chapas para que estas se acomodassem adequadamente ao desenho da sacada.
Como o espaço era de 215mm por 215mm, esta foi a área removida. A conta aqui foi feita da ordem inversa: Dado o desenho da sacada, retirando-se 65mm de espaçamento para as paredes e 165mm para o fechamento com vidro, o corte seria feito com 50mm na face voltada para o fechamento (165mm + 50mm = 215mm) e com 215mm na face voltada para a parede (isso por si só funciona pois o espaçamento de 50mm acompanharia o deslocamento de 215mm, você vai entender nas imagens).
OBS.: Nas fotos da execução vocês perceberão que o projeto final não acompanhou este planejamento. Erro de execução, acontece!
Cálculo do posicionamento dos furos para as bolas de tênis, fixação e transporte
Posição das bolas de tênis
Após determinado o desenho do tablado em si, fazia-se necessário calcular a distribuição das bolas de tênis ao longo do mesmo.
Como eu disse anteriormente (preste atenção!), não é interessante que as bolas fiquem mais de 500mm distantes uma das outras.
Aí o jênio matemático de plantão (sim, com ‘J’ mesmo!) vai dizer: “Fácil, basta desenhar então linhas a cada 500mm na largura e comprimento e colocar as bolinhas onde as linhas se cruzarem!”
Calma, Horácio (cabeção!), existem alguns pontos a se considerar:
- O primeiro é o mais óbvio, se você desenhar linhas a cada 500mm, as bolas estarão com distância nas diagonais igual a 500mm * sqrt(2) (não sei desenhar raiz nessa fita mesmo, e daí?!). Isso é maior que 500mm ferindo a regra que diz que as bolas não podem estar mais distantes que isso de suas vizinhas imediatas.
- O segundo ponto é que você não pode começar medindo do milímetro zero, do exato canto das chapas de compensado. Você precisa de um espaço mínimo para o diâmetro do furo que servirá de berço para a bola sem que seja comprometida a estrutura das chapas
- E o terceiro ponto é que, com o desconto do espaço acima, esta distribuição pode não ser ideal.
Então vamos lá. Se fosse um retângulo, as chapas mediriam 2200mm x 1250mm como já calculamos anteriormente. Removendo-se 100mm de cada lado para espaçamento adequado, teríamos as medidas 2000mm x 1230mm.
Para os 2000mm é ótimo: 5 bolinhas, uma a cada 500mm e acabou! (a divisão dá 4, eu sei, coração! Mas este é o número de intervalos. É preciso mais uma bola na ponta);
Agora, para os 1230mm é mais complexo. 1230mm / 500mm = 2,46 intervalos. Isso complicaria muito a conta e a execução.
Sendo assim, preferi arredondar o número para cima (sobrar apoio é melhor que faltar, aqui) e trabalhar com 4 bolas ou três espaços. O resultado final ficou o de uma bola a cada 333,33mm, então coloquei um espaço com 340mm e dois com 330mm.
Legal, até então tudo maravilhoso, mas lembre-se: O desenho do tablado não é um retângulo perfeito! E como se der chuva de Xuxa, no meu colo cai Pelé, é claro que exatamente naquela remoção teria o espaço de uma bola.
Como calcular um novo espaço para ela de forma a manter a boa distribuição dos apoios? É prudente colocar a posição na diagonal entre a posição inicial e a bola mais próxima, mas a que distância? Eu calculei a média entre 500mm e 333,33mm e cheguei ao número 420mm.
Ótimo, posição das bolas determinadas, o próximo passo era determinar a posição de outras furações auxiliares.
Posição dos furos de fixação
É muito pertinente fixar uma chapa de compensado à outra para evitar que a superior deslize sobre as bolas e também para evitar que, ao se aplicar peso em uma das extremidades da chapa superior, esta levantaria na extremidade oposta, permitindo deslocamento das bolas em baixo. Além disso, esta manobra facilita manutenções e limpeza sob o tablado, permitindo que o mesmo seja erguido como um todo para tais atividades.
Esta fixação precisava ser feita com algo resistente e maleável para aguentar as ondulações do tablado sem se romper. A escolha foi por fitas tied-up de 10mm de espessura (o famoso enforca-gato!).
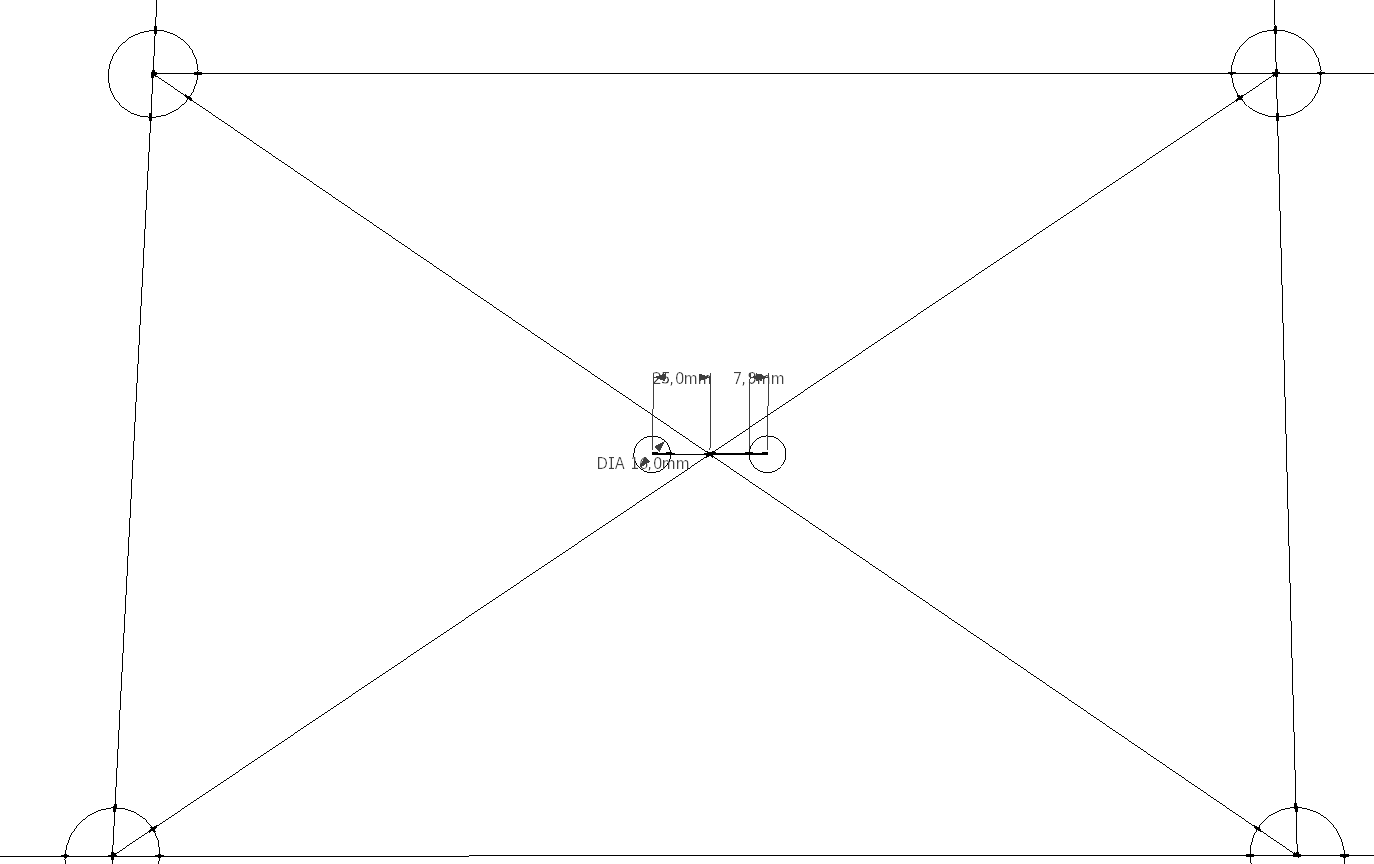
A posição dos furos foi calculada da seguinte forma: entre 4 bolas mais próximas a cada extremidade do tablado, tracei as diagonais do quadrilátero formado por elas e, descoberto o cruzamento das retas, de forma paralela ao comprimento, afastei 25mm e marquei as posições que seriam para os furos de 10mm. Assim, cada furo ficaria 50mm longe um do outro não afetando a integridade e estrutura da chapa.
Figura 3 - Furos para fixação
Posição das alças para transporte
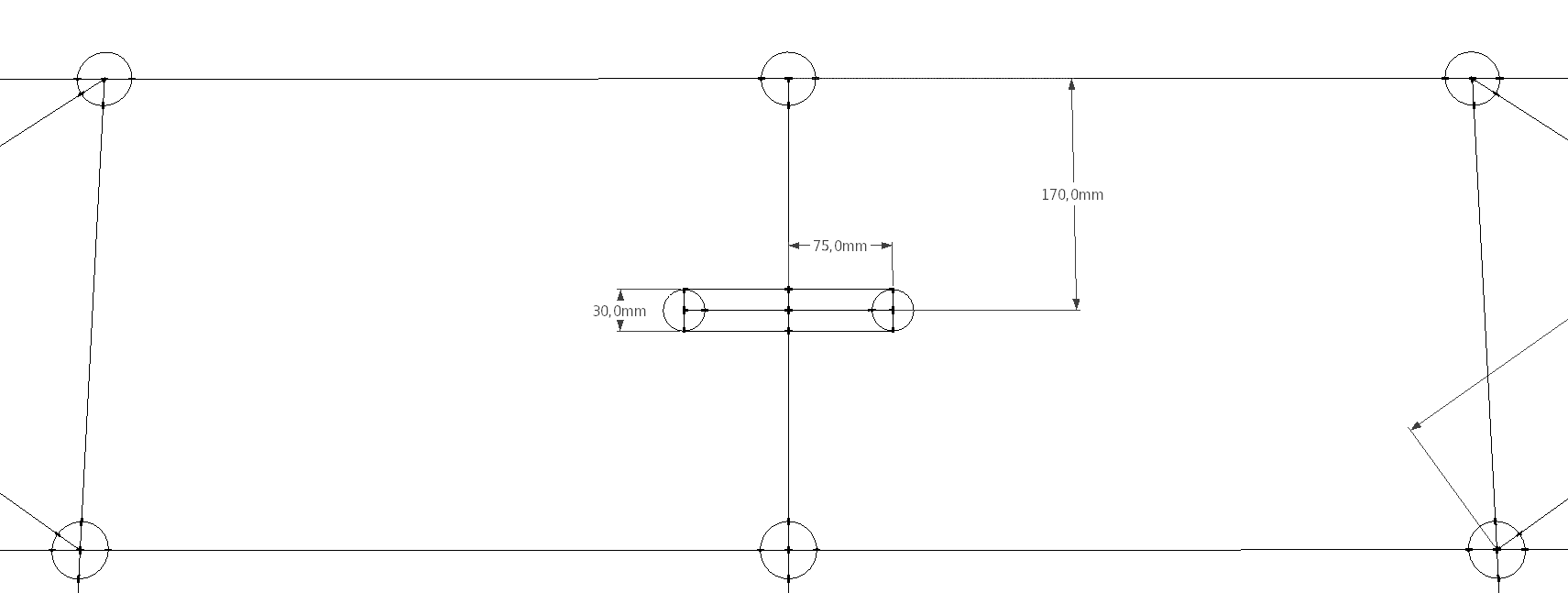
Outra furação auxiliar seria a elaboração de alças de transporte. Estas seriam localizadas sobre a linha do meio no comprimento e nos primeiro e terceiro quadriláteros da largura. Ficariam centralizados em largura e comprimento medindo 150mm x 30mm e com cantos arredondados conforme imagem abaixo:
Figura 4 - Alça para transporte
Isso porque não seria tarefa fácil carregar uma chapa dessas dimensões caso precisasse executar a tarefa sozinho. Além disso, estas alças auxiliam no transporte e manutenção sob o tablado da mesma forma que acima.
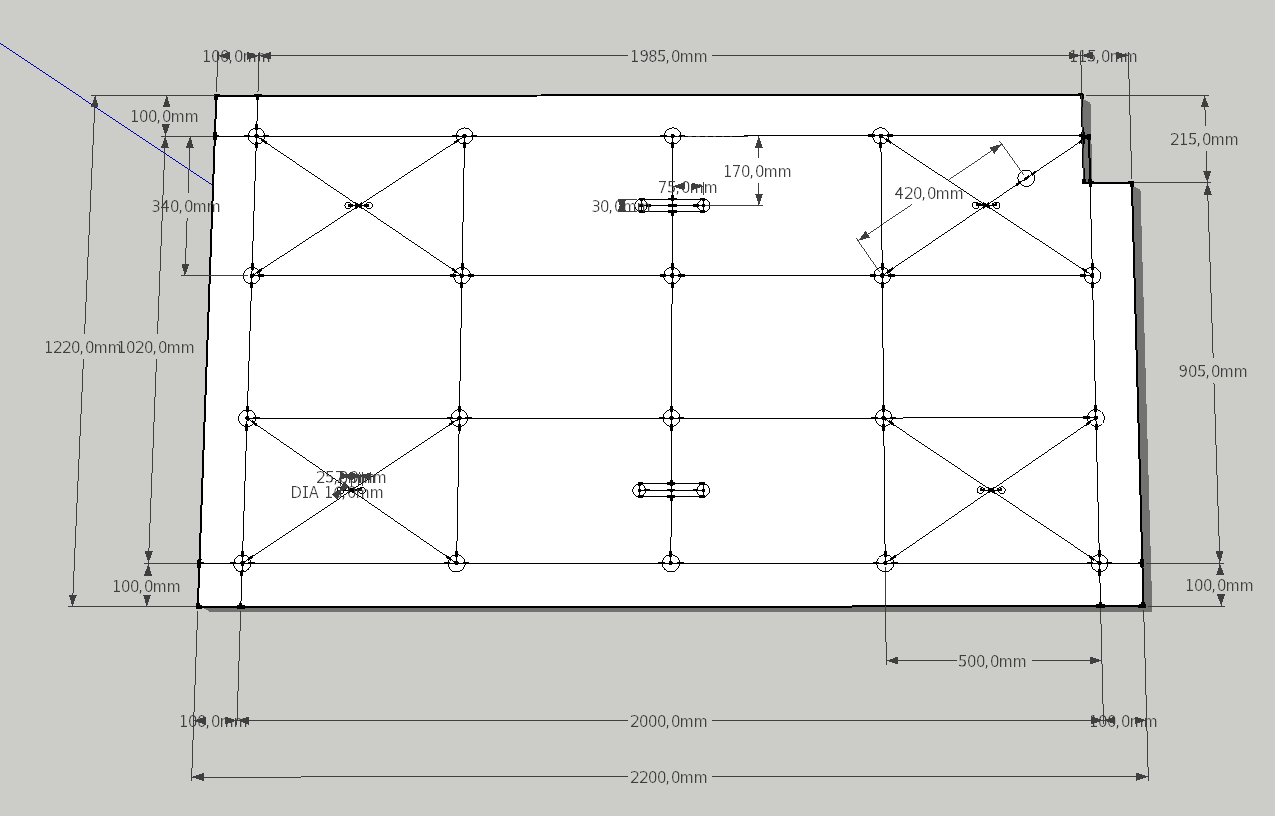
Desta forma, o resultado final de todas as medidas ficou sendo o seguinte:
Figura 5 - Medidas completas do tablado
Fiquem espertos para a Parte II onde eu abordarei a construção da bagaça. Na Parte III falarei da instalação da bodega propriamente dita!
Nenhum comentário :
Postar um comentário